计算机系统概论
计算机系统由软件和硬件两大部分组成
计算机的基本组成
计算机由运算器、存储器、控制器、输入设备和输出设备五大部件组成。
计算机结构图
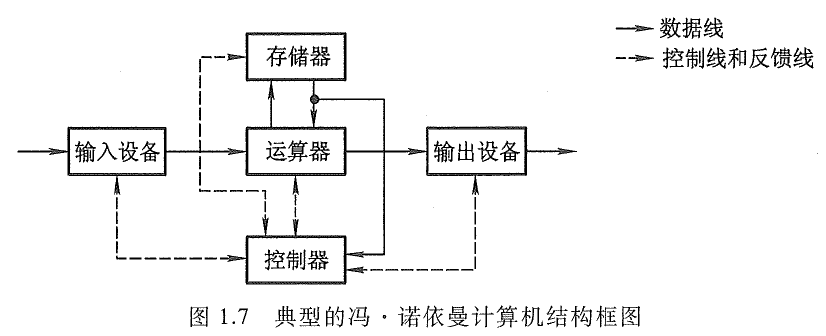 | 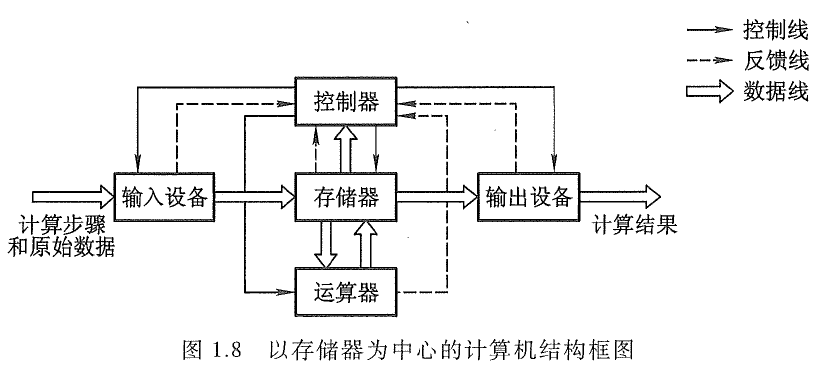 | 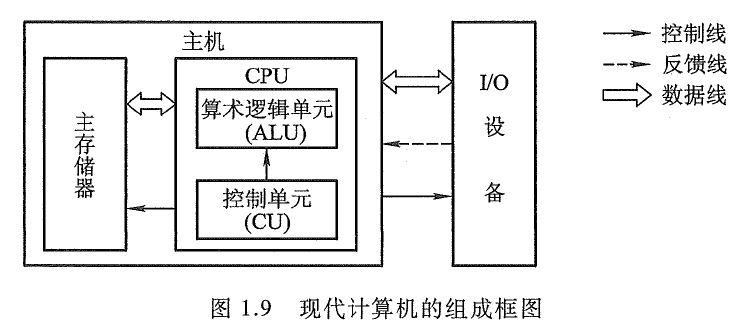 |
|---|
现代计算机结构及工作步骤
算术逻辑单元
ALU:用来完成算术逻辑运
控制单元
CU:用来解释存储器中的指令,并发出各种操作命令来执行指令
寄存器
寄存器:寄存器的功能是存储二进制代码,它是由具有存储功能的触发器组合起来构成的。一个触发器可以存储1位二进制代码,故存放n位二进制代码的寄存器,需用n个触发器来构成。

名词解释:
计算机硬件组成原理名词解释 CPU、PC、IR、CU、ALU、ACC、MQ、X、MAR、MDR、I/O、MIPS、CPI、FLOPS
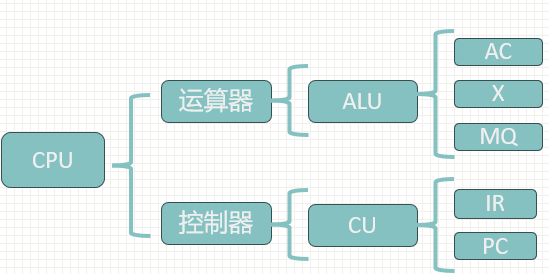
- CPU:Central Processing Unit,处理机(器),是计算机硬件的核心部件,主要由运算器和控制器组成。
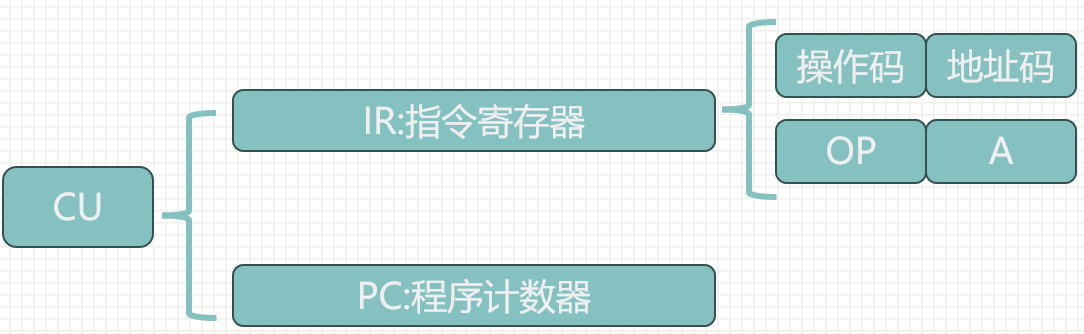
- PC:Program Counter,程序计数器,其功能是存放当前欲执行指令的地址,并可自动计数形成下一条指令地址。
- IR:Instruction Register,指令寄存器,其功能是存放当前正在执行的指令。
- CU:Control Unit,控制单元(部件),为控制器的核心部件,其功能是产生微操作命令序列。
- ALU:Arithmetic Logic Unit,算术逻辑运算单元,为运算器的核心部件,其功能是进行算术、逻辑运算。
- ACC:Accumulator,累加器,是运算器中既能存放运算前的操作数,又能存放运算结果的寄存器。
- MQ:Multiplier-Quotient Register,乘商寄存器,乘法运算时存放乘数、除法时存放商的寄存器。
- X:此字母没有专指的缩写含义,可以用作任一部件名,在此表示操作数寄存器,即运算器中工作寄存器之一,用来存放操作数;
- MAR:Memory Address Register,存储器地址寄存器,在主存中用来存放欲访问的存储单元的地址。
- MDR:Memory Data Register,存储器数据缓冲寄存器,在主存中用来存放从某单元读出、或要写入某存储单元的数据。
- I/O:Input/Output equipment,输入/输出设备,为输入设备和输出设备的总称,用于计算机内部和外界信息的转换与传送。
- MIPS:Million Instruction Per Second,每秒执行百万条指令数,为计算机运算速度指标的一种计量单位。
- CPI:执行一条指令所需的时钟周期(机器主频的倒数)。
- FLOPS:浮点运算次数每秒。
 |  |  |
|---|
工作步骤

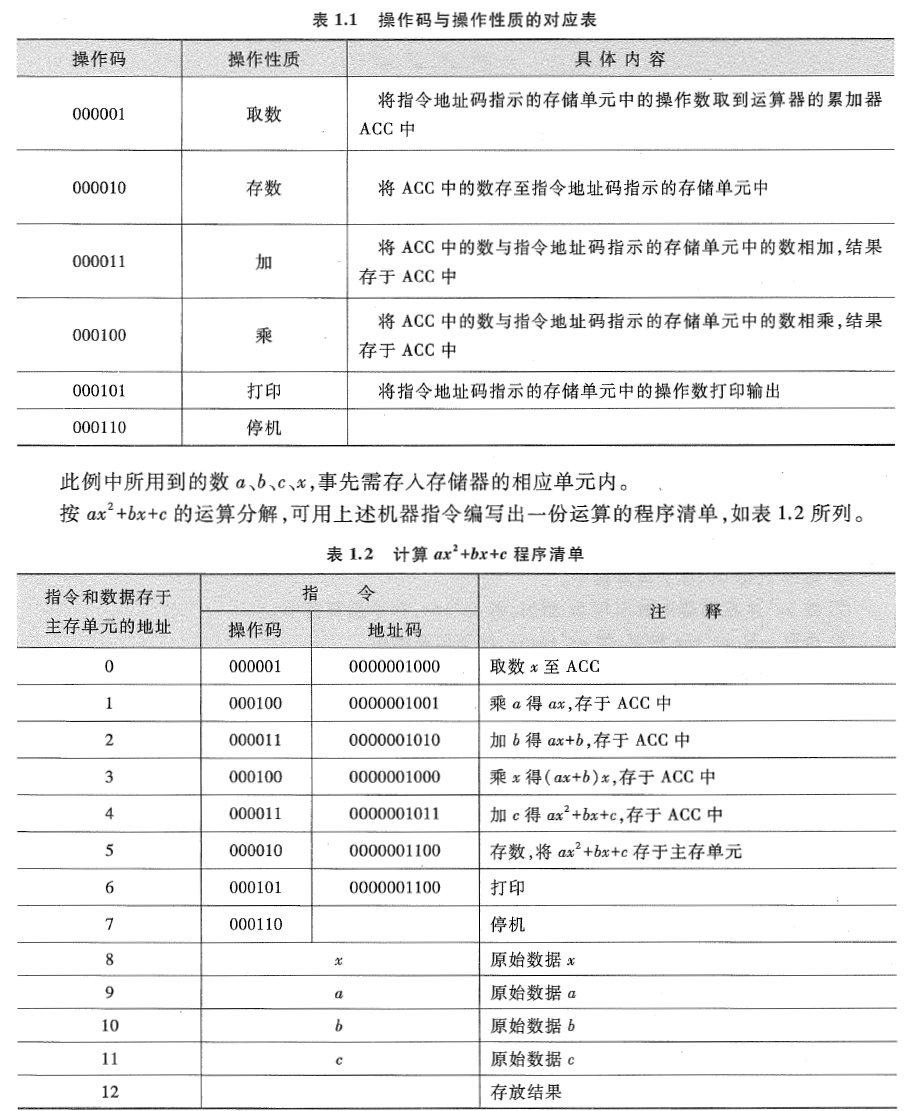
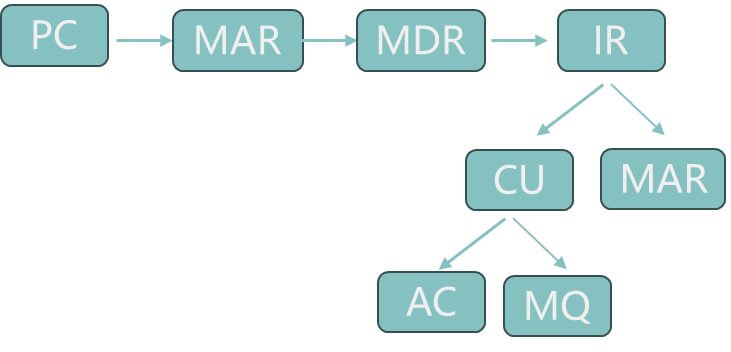
执行过程
计算机硬件的主要技术指标
机器字长: 机器字长是指CPU 一次能处理数据的位数
- 机器(计算机)字长:等于MDR(存储器数据寄存器)的位数,通常为8的整数倍
- 指令字长:指令=操作+数据地址,冯诺依曼计算机体系采用的是‘存储程序’根本特征,因此指令在运行时会存储在MDR当中,因此一般来说,指令字长=机器(计算机)字长
- 存储字长:同理,数据暂存在MDR当中,存储字长=MDR位数
- 数据字长:指计算机的数据总线一次可以传递的位数,通常大于MDR位数
计算机的运算方法
学习引入
进制转换
B:二进制 D:十进制 O:八进制 H:十六进制

数据存储
本章讲述 计算机的运算方法,为了运算我们需要存储数据,那么计算机的数据是如何存储的?
以字节方式存储
无符号数和有符号数
无符号数
计算机中的数均放在寄存器中,通常称寄存器的位数为机器字长。所谓无符号数,即没有符号的数,在寄存器中的每一位均可用来存放数值。当存放有符号数时,则需留出位置存放符号。
因此,在机器字长相同时,无符号数与有符号数所对应的数值范围是不同的。以机器字长为8位为例,无符号数的表示范围为0~255(共256个) ,而有符号数的表示范围为- 127 ~ +127(共255个)【少了一个的原因是 0的特殊存在】
有符号数
定点数
正负表示
0表示正数,1表示负数
小数点表示
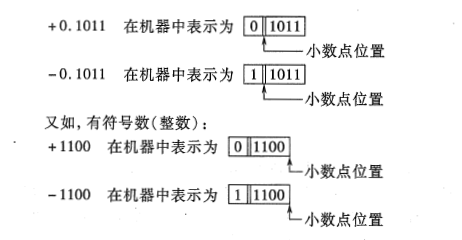
原码表示
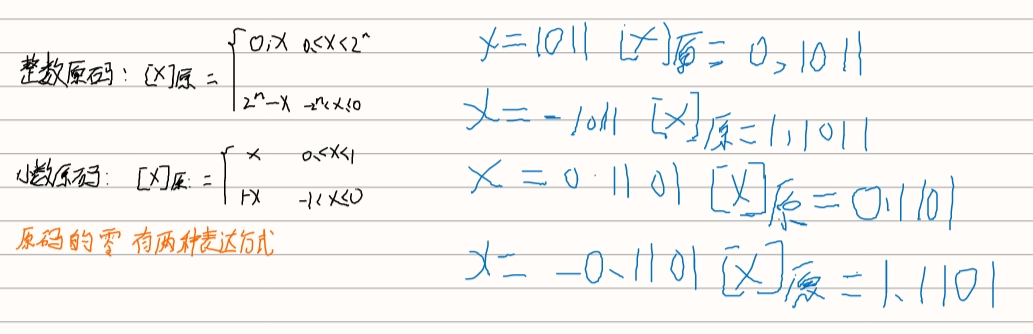
由于原码只是方便表示,简单明了,使用原码进行加减运算时,却带来了许多麻烦。例如,当两个操作数符号不同且要做加法运算时,先要判断两数绝对值大小,然后将绝对值大的数减去绝对值小的数,结果的符号以绝对值大的数为准,因此补码是很好的选择
补码表示

原码——>补码
数值位按位取反,末尾+1
整数:负的补码,先补0,再取反求补码
小数:负的补码,先求补码,再补0
反码
直接取反
移码

浮点数
浮点数
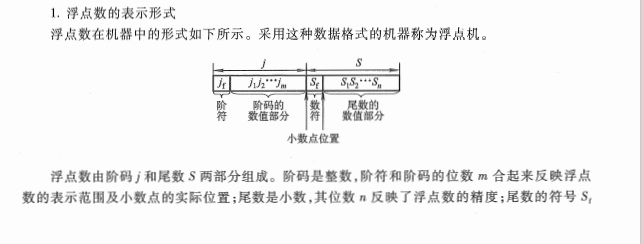
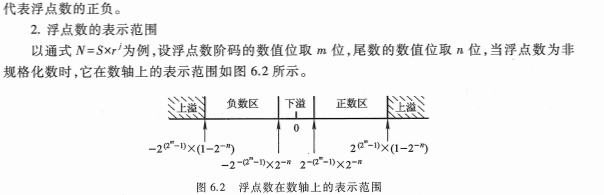
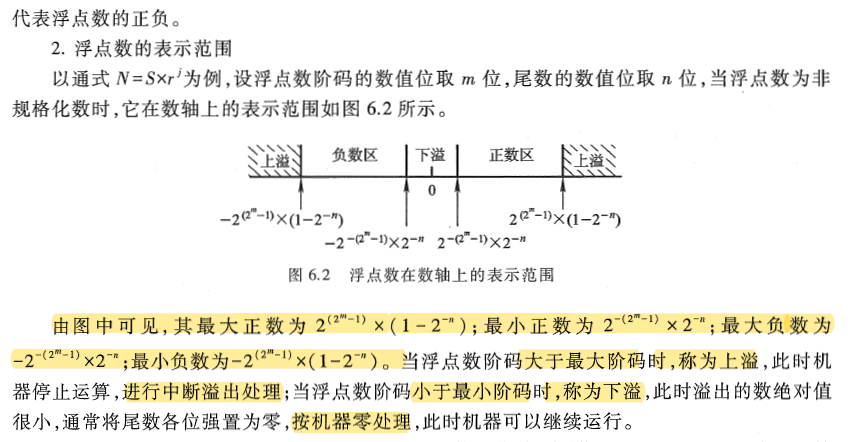
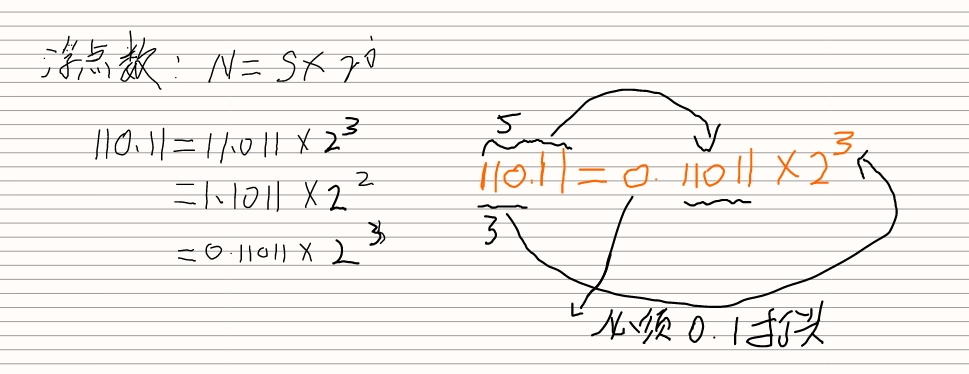
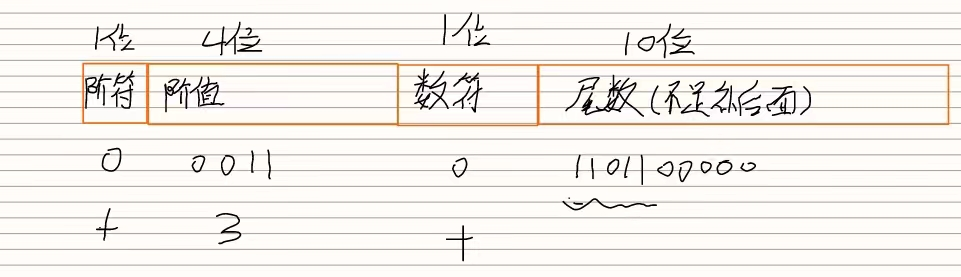
IEEE 754 标准
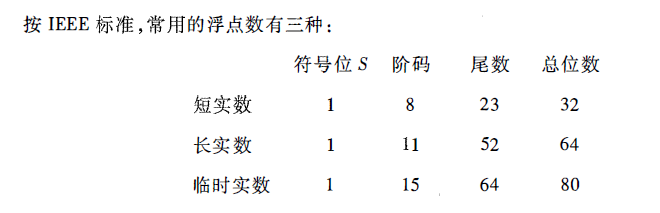
它表示浮点数的正负,但与其有效位(尾数)是分开的。 阶码用移码表示,阶码的真值都被加上一个常数(偏移量)
- 规格化:首位为1,
- 阶码为移码,+127,+1023 …… 即2的n次方-1,n是移码的数值位
定点运算
定点运算包括,移位、加、减、乘、除。
移位运算
本科目介绍的主要是算术移位
规则
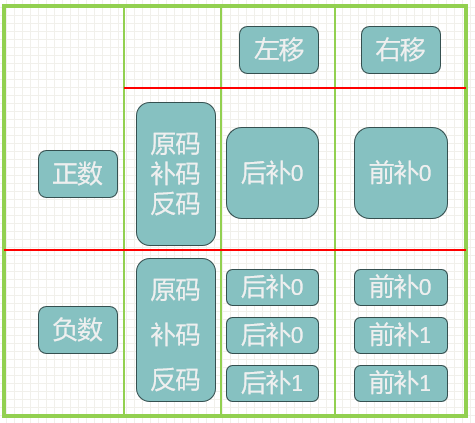
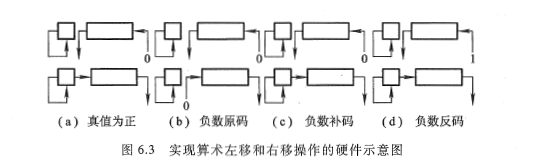
加法与减法运算
公式

溢出
溢出的三种判断方法
- 结果符号判断
- 双符号位判断
- 符号位+数值位最高位判断

原码一位乘

原码二位乘

补码乘法

除法运算
恢复余数法
