时间复杂度和空间复杂度

算法效率的度量方法

1. 算法采用的策略，方案
2. 编译产生的代码质量
3. 问题的输入规模
4. 机器执行指令的速度

抛开这些与计算机硬件、软件有关的因素，一个程序的运行时间依赖于算法的好坏和问题的输入规模。 （所谓的问题输入规模是指输入量的多少)

算法分析

暴力枚举	高斯算法

第一种算法执行了 1+(n+1)+n=2n+2次

第二种算法，是1+1=2次

如果我们把循环看做一个整体，忽略头尾判断的开销，那么这两个算法其实就是n和1的差距。

算法研究原则

我们不关心编写程序所用的语言是什么，也不关心这些程序将跑在什么样的计算机上，我们只关心它所实现的算法

使用抽象的方法进行研究

算法分析总结

判断一个算法的效率时，函数中的常数和其他次要项常常可以忽略，而更应该关注主项（最高项）的阶数

时间复杂度

算法时间复杂度的定义：在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析 T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度，也就是算法的时间量度，记作： T(n)= O(f(n))。 它表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。 其中f(n)是问题规模n的某个函数。

执行次数==时间

大O阶方法

1. 用常数1取代运行时间中的所有加法常数。
2. 在修改后的运行次数函数中，只保留最高阶项。
3. 如果最高阶项存在且不是1，则去除与这个项相乘的常数。
4. 得到的最后结果就是大0阶。

常数阶

即O(1)

printf("123");
printf("123");
printf("123");

线性阶

即O(n)

int i = 0;
int sum = 0;
int n = 100;
for(i=1;i <=n;i++){
sum = sum + i;
}

因为循环体中的代码需要执行n次

平方阶

即O(n^2)

int i,j;
for(i=1;i <=n;i++){
    for(j = i;j<=n;j++){
       printf("123"); 
    }
  }

对数阶

int i = 1，n = 100;
while(i<n){
    i = i * 2;
}

举例

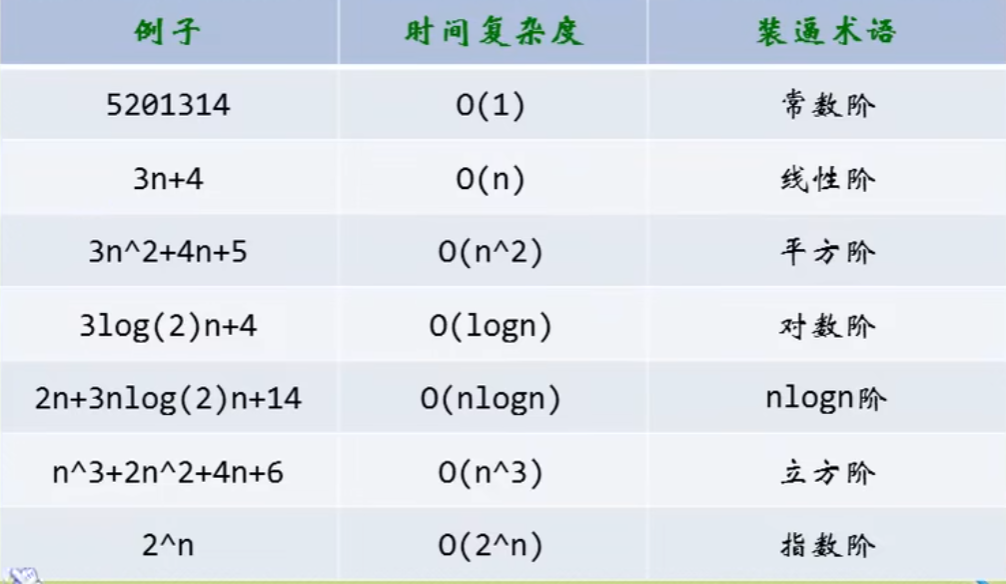
空间复杂度

算法的空间复杂度通过计算算法所需的存储空间实现，算法的空间复杂度的计算公式记作：S(n)=O(f(n))， 其中，n为问题的规模， f(n)为语句关于n所占存储空间的函数。

通常，我们都是用“时间复杂度”来指运行时间的需求，是用“空间复杂度”指空间需求。当直接要让我们求“复杂度”时，通常指的是时间复杂度。