数学知识
质数
判素数
bool is_prime(int x) {
if (x < 2) return false;
for (int i = 2; i <= x / i; i++)
if (x % i == 0)
return false;
return true;
}分解质因数
分解质因数------试除法.(用到的原理:唯一分解定理(算数基本定理))
特别要注意------分解质因数与质因数不一样
分解质因数是一个过程,而质因数是一个数.
一个合数分解而成的质因数最多只包含一个大于sqrt(n)的质因数
(反证法,若n可以被分解成两个大于sqrt(n)的质因数,则这两个质因数相乘的结果大于n,与事实矛盾).
当枚举到某一个数i的时候,n的因子里面已经不包含2-i-1里面的数,如果n%i==0,则i的因子里面也已经不包含2-i-1里面的数,因此每次枚举的数都是质数.
算数基本定理(唯一分解定理):任何一个大于1的自然数N,如果N不为质数,那么N可以唯一分解成有限个质数的乘积 N=P~1~^a1^P~2~ ^a2^P~3~^a3^......P~n~^an^,这里P~1~<P~2~<P~3~......<P~n~均为质数,其中指数ai是正整数。这样的分解称为 N 的标准分解式。最早证明是由 欧几里得给出的,由陈述证明。此定理可推广至更一般的交换代数和代数数论。
质因子(或质因数)在数论里是指能整除给定正整数的质数。根据算术基本定理,不考虑排列顺序的情况下,每个正整数都能够以唯一的方式表示成它的质因数的乘积。
两个没有共同质因子的正整数称为互质。因为1没有质因子,1与任何正整数(包括1本身)都是互质。
只有一个质因子的正整数为质数。
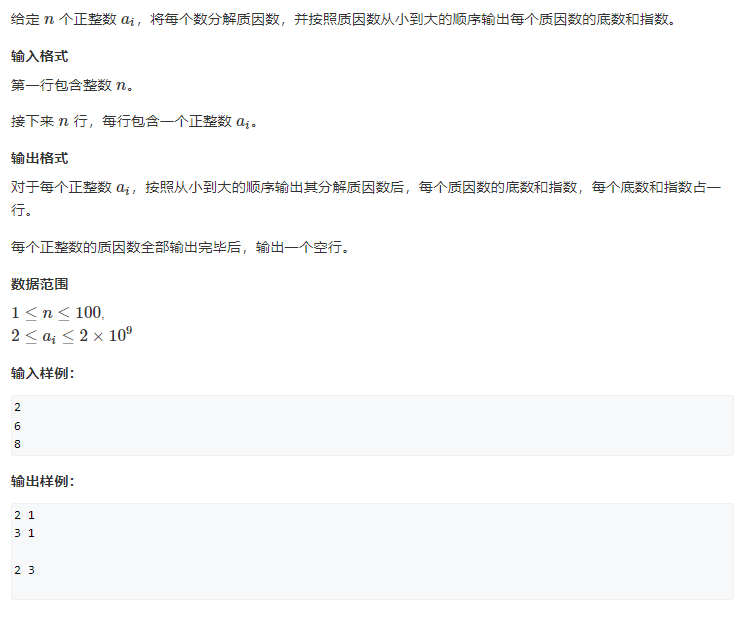
void divide(int x) {
for (int i = 2; i <= x / i; i++)
if (x % i == 0) {
int s = 0;
while (x % i == 0) x /= i, s++;
cout << i << ' ' << s << endl;
}
if (x > 1) cout << x << ' ' << 1 << endl;
cout << endl;
}筛质数
朴素筛法
- 做法:把2~(n-1)中的所有的数的倍数都标记上,最后没有被标记的数就是质数.
- 原理:假定有一个数p未被2
~(p-1)中的数标记过,那么说明,不存在2~(p-1)中的任何一个数的倍数是p,也就是说p不是2~(p-1) 中的任何数的倍数,也就是说2~(p-1)中不存在p的约数,因此,根据质数的定义可知:p是质数. - 调和级数:当n趋近于正无穷的时候,1/2+1/3+1/4+1/5+…+1/n=lnn+c.(c是欧阳常数,约等于0.577左右.)
- 底数越大,log数越小
- 时间复杂度:约为O(nlogn);(注:此处的log数特指以2为底的log数).
埃氏筛(稍加优化版的筛法).
- 质数定理:1~n中有n/lnn个质数.
- 原理:在朴素筛法的过程中只用质数项去筛.
- 时间复杂度:粗略估计:O(n).实际:O(nlog(logn)).
- 1~n中,只计算质数项的话,
1/2+1/3+1/4+1/5+…+1/n的大小约为log(logn).
线性筛
若n在10的6次方的话,线性筛和埃氏筛的时间效率差不多,若n在10的7次方的话,线性筛会比埃氏筛快了大概一倍.
核心:1~n内的合数p只会被其最小质因子筛掉.
原理:1~n之内的任何一个合数一定会被筛掉,而且筛的时候只用最小质因子来筛,然后每一个数都只有一个最小质因子,因此每个数都只会被筛一次,因此线性筛法是线性的.
枚举到i的最小质因子的时候就会停下来,即
if(i%primes[j]==0) break;.因为从小到大枚举的所有质数,所以当
i%primes[j]!=0时,primes[j]一定小于i的最小质因子,primes[j]一定是primes[j] i的最小质因子.因为是从小到大枚举的所有质数,所以当
i%primes[j]==0时,primes[j]一定是i的最小质因子,而primes[j]又是primes[j] 的最小质因子,因此primes[j]是iprimes[j]的最小质因子.关于for循环的解释:
首先要把握住一个重点:我们枚举的时候是从小到大枚举的所有质数
当i%primes[j]
==0时,因为是从小到大枚举的所有质数,所以primes[j]就是i的最小质因子,而primes[j]又是其本身primes[j]的最小质因子,因此当i%primes[j]==0时,primes[j]是primes[j]i的最小质因子.
当i%primes[j]!=0时,因为是从小到大枚举的所有质数,且此时并没有出现过有质数满足i%primes[j] ==0,因此此时的primes[j]一定小于i的最小质因子,而primes[j]又是其本身primes[j]的最小质因子,所以当i%primes[j]! =0时,primes[j]也是primes[j]i的最小质因子.
综合1,2得知,在内层for循环里面无论何时,primes[j]都是primes[j]i的最小质因子,因此”st[primes[j]i] =true”语句就是用primes[j]i这个数的最小质因子来筛掉这个数.
大于10^7^ 线性筛法要快一倍
约数
试除法求约数
vector<int> get_divisors(int x) {
vector<int> res;
for (int i = 1; i <= x / i; i++)
if (x % i == 0) {
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());
return res;
}约数个数和约数之和
如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数:(c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和:(p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
//个数
typedef long long LL;
const int mod = 1e9+7;
unordered_map <int,int> primes;
void num_divisors(int x)
{
cin>>x;
for(int i = 2;i<=x/i;i++)
{
while(x%i == 0)
{
x /=i;
primes[i]++;
}
if(x > 1) primes[x]++;
}
LL res = 1;
for(auto prime:primes) res = res*(prime.second+1) %mod;
cout<<res<<endl;
}//约数之和
typedef long long LL;
const int mod = 1e9+7;
unordered_map <int,int> primes;
void sum_divisors(int x)
{
cin>>x;
for(int i = 2;i<=x/i;i++)
{
while(x%i == 0)
{
x /=i;
primes[i]++;
}
if(x > 1) primes[x]++;
}
LL res = 1;
for(auto prime:primes)
{
int p = prime.first, q = prime.second;
LL t = 1;
while(q--)
{
t = (t*p+1)%mod;
res = res * t % mod; //秦九邵算法
}
}
cout<<res<<endl;
}欧几里得算法(辗转相除法)
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}欧拉函数
快速幂
扩展欧几里得算法
中国剩余定理
高斯消元
求组合数
容斥原理
模板
试除法判定质数
bool is_prime(int x) {
if (x < 2) return false;
for (int i = 2; i <= x / i; i++)
if (x % i == 0)
return false;
return true;
}试除法分解质因数
void divide(int x) {
for (int i = 2; i <= x / i; i++)
if (x % i == 0) {
int s = 0;
while (x % i == 0) x /= i, s++;
cout << i << ' ' << s << endl;
}
if (x > 1) cout << x << ' ' << 1 << endl;
cout << endl;
}朴素筛法求素数(埃氏)
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (st[i]) continue;
primes[cnt++] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}线性筛法求素数
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (!st[i]) primes[cnt++] = i;
for (int j = 0; primes[j] <= n / i; j++) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) break; //primes[j] 一定是i的最小质因子
}
}
}试除法求所有约数
vector<int> get_divisors(int x) {
vector<int> res;
for (int i = 1; i <= x / i; i++)
if (x % i == 0) {
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());
return res;
}约数个数和约数之和
如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数:(c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和:(p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
//个数
typedef long long LL;
const int mod = 1e9+7;
unordered_map <int,int> primes;
void num_divisors(int x)
{
cin>>x;
for(int i = 2;i<=x/i;i++)
{
while(x%i == 0)
{
x /=i;
primes[i]++;
}
if(x > 1) primes[x]++;
}
LL res = 1;
for(auto prime:primes) res = res*(prime.second+1) %mod;
cout<<res<<endl;
}//约数之和
typedef long long LL;
const int mod = 1e9+7;
unordered_map <int,int> primes;
void sum_divisors(int x)
{
cin>>x;
for(int i = 2;i<=x/i;i++)
{
while(x%i == 0)
{
x /=i;
primes[i]++;
}
if(x > 1) primes[x]++;
}
LL res = 1;
for(auto prime:primes)
{
int p = prime.first, q = prime.second;
LL t = 1;
while(q--)
{
t = (t*p+1)%mod;
res = res * t % mod; //秦九邵算法
}
}
cout<<res<<endl;
}欧几里得算法
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}求欧拉函数
int phi(int x) {
int res = x;
for (int i = 2; i <= x / i; i++)
if (x % i == 0) {
res = res / i * (i - 1);
while (x % i == 0) x /= i;
}
if (x > 1) res = res / x * (x - 1);
return res;
}筛法求欧拉函数
int primes[N], cnt; // primes[]存储所有素数
int euler[N]; // 存储每个数的欧拉函数
bool st[N]; // st[x]存储x是否被筛掉
void get_eulers(int n) {
euler[1] = 1;
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes[cnt++] = i;
euler[i] = i - 1;
}
for (int j = 0; primes[j] <= n / i; j++) {
int t = primes[j] * i;
st[t] = true;
if (i % primes[j] == 0) {
euler[t] = euler[i] * primes[j];
break;
}
euler[t] = euler[i] * (primes[j] - 1);
}
}
}快速幂
求 m^k mod p,时间复杂度 O(logk)。
int qmi(int m, int k, int p) {
int res = 1 % p, t = m;
while (k) {
if (k & 1) res = res * t % p;
t = t * t % p;
k >>= 1;
}
return res;
}扩展欧几里得算法
// 求x, y,使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y) {
if (!b) {
x = 1;
y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= (a / b) * x;
return d;
}高斯消元
// a[N][N]是增广矩阵
int gauss() {
int c, r;
for (c = 0, r = 0; c < n; cpp) {
int t = r;
for (int i = r; i < n; i++)
// 找到绝对值最大的行
if (fabs(a[i][c]) > fabs(a[t][c]))
t = i;
if (fabs(a[t][c]) < eps) continue;
// 将绝对值最大的行换到最顶端
for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]);
// 将当前行的首位变成1
for (int i = n; i >= c; i--) a[r][i] /= a[r][c];
// 用当前行将下面所有的列消成0
for (int i = r + 1; i < n; i++)
if (fabs(a[i][c]) > eps)
for (int j = n; j >= c; j--)
a[i][j] -= a[r][j] * a[i][c];
r++;
}
if (r < n) {
for (int i = r; i < n; i++)
if (fabs(a[i][n]) > eps)
// 无解
return 2;
// 有无穷多组解
return 1;
}
for (int i = n - 1; i >= 0; i--)
for (int j = i + 1; j < n; j++)
a[i][n] -= a[i][j] * a[j][n];
return 0; // 有唯一解
}递推法求组合数
// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;通过预处理逆元的方式求组合数
首先预处理出所有阶乘取模的余数fact[N],以及所有阶乘取模的逆元infact[N]
如果取模的数是质数,可以用费马小定理求逆元
// 快速幂模板
int qmi(int a, int k, int p) {
int res = 1;
while (k) {
if (k & 1) res = (LL) res * a % p;
a = (LL) a * a % p;
k >>= 1;
}
return res;
}
// 预处理阶乘的余数和阶乘逆元的余数
int main() {
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i++) {
fact[i] = (LL) fact[i - 1] * i % mod;
infact[i] = (LL) infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
}Lucas定理
若p是质数,则对于任意整数 1 <= m <= n,有:
C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)
// 快速幂模板
int qmi(int a, int k, int p) {
int res = 1 % p;
while (k) {
if (k & 1) res = (LL) res * a % p;
a = (LL) a * a % p;
k >>= 1;
}
return res;
}
// 通过定理求组合数C(a, b)
int C(int a, int b, int p) {
if (a < b) return 0;
// x是分子,y是分母
LL x = 1, y = 1;
for (int i = a, j = 1; j <= b; i--, j++) {
x = (LL) x * i % p;
y = (LL) y * j % p;
}
return x * (LL) qmi(y, p - 2, p) % p;
}
int lucas(LL a, LL b, int p) {
if (a < p && b < p) return C(a, b, p);
return (LL) C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}分解质因数法求组合数
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
- 筛法求出范围内的所有质数
- 通过
C(a, b) = a! / b! / (a - b)!这个公式求出每个质因子的次数。 n! 中p的次数是n / p + n / p^2 + n / p^3 + ... - 用高精度乘法将所有质因子相乘
int primes[N], cnt; // 存储所有质数
int sum[N]; // 存储每个质数的次数
bool st[N]; // 存储每个数是否已被筛掉
// 线性筛法求素数
void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (!st[i]) primes[cnt++] = i;
for (int j = 0; primes[j] <= n / i; j++) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
// 求n!中的次数
int get(int n, int p) {
int res = 0;
while (n) {
res += n / p;
n /= p;
}
return res;
}
// 高精度乘低精度模板
vector<int> mul(vector<int> a, int b) {
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i++) {
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t) {
c.push_back(t % 10);
t /= 10;
}
return c;
}
int main() {
// 预处理范围内的所有质数
get_primes(a);
// 求每个质因数的次数
for (int i = 0; i < cnt; i++) {
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}
vector<int> res;
res.push_back(1);
// 用高精度乘法将所有质因子相乘
for (int i = 0; i < cnt; i++)
for (int j = 0; j < sum[i]; j++)
res = mul(res, primes[i]);
}卡特兰数
给定n个0和n个1,它们按照某种顺序排成长度为2n的序列,
满足任意前缀中0的个数都不少于1的个数的序列的数量为:Cat(n) = C(2n, n) / (n + 1)
NIM游戏
给定N堆物品,第i堆物品有Ai个。两名玩家轮流行动,每次可以任选一堆,取走任意多个物品,可把一堆取光,但不能不取。取走最后一件物品者获胜。两人都采取最优策略,问先手是否必胜。
我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手,第二个行动的称为后手。若在某一局面下无论采取何种行动,都会输掉游戏,则称该局面必败。
所谓采取最优策略是指,若在某一局面下存在某种行动,使得行动后对面面临必败局面,则优先采取该行动。同时,这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况,即两人均无失误,都采取最优策略行动时游戏的结果。
NIM博弈不存在平局,只有先手必胜和先手必败两种情况。
定理: NIM博弈先手必胜,当且仅当 A1 ^ A2 ^ … ^ An != 0
公平组合游戏ICG
若一个游戏满足:
- 由两名玩家交替行动;
- 在游戏进程的任意时刻,可以执行的合法行动与轮到哪名玩家无关;
- 不能行动的玩家判负;
则称该游戏为一个公平组合游戏。
NIM博弈属于公平组合游戏,但城建的棋类游戏,比如围棋,就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子,胜负判定也比较复杂,不满足条件2和条件3。
有向图游戏
给定一个有向无环图,图中有一个唯一的起点,在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动,每次可以移动一步,无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是,把每个局面看成图中的一个节点,并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。
Mex运算
设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算,即: mex(S) = min{x}, x属于自然数,且x不属于S
SG函数
在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1, y2, …, yk,定义SG(x)为x的后继节点y1, y2, …, yk 的SG函数值构成的集合再执行mex(S)运算的结果,即:SG(x) = mex({SG(y1), SG(y2), …, SG(yk)})
特别地,整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即SG(G) = SG(s)。
有向图游戏的和
设G1, G2, …, Gm 是m个有向图游戏。定义有向图游戏G,它的行动规则是任选某个有向图游戏Gi,并在Gi上行动一步。G被称为有向图游戏G1, G2, …, Gm的和。
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和,即: SG(G) = SG(G1) ^ SG(G2) ^ … ^ SG(Gm)
定理
有向图游戏的某个局面必胜,当且仅当该局面对应节点的SG函数值大于0。 有向图游戏的某个局面必败,当且仅当该局面对应节点的SG函数值等于0。