1.快速排序
1.1快速排序

c
#include<stdio.h>
int n;
int q[1000];
void quick_sort(int q[],int l,int r)
//将数组q,数组首尾下标l,r输入快排函数quick_sort
{
if(l>=r)return;
//如果lr交叉,则说明数列已经被分割成单元素数列,排序完毕
int x=q[(l+r)/2];
//将数组中间位数值作为分界基准x
int i=l-1;
//设置从数组首位开始计数的指针i
int j=r+1;
//设置从数组末尾开始计数的指针j
while(i<j)
//在指针交叉前遍历一遍数组,将小于x的值置于左侧,大于x的值置于右侧
{
do i++;while(q[i]<x);
//当i指向的数值小于分界基准x时继续向后移动
//如数值大于x,则扣留当前元素,跳转到j指针
do j--;while(q[j]>x);
//当j指向的数值大于分界基准x时继续向前移动
//当数值小于x,则将其与之前扣留的元素互换
if(i<j)
//如果指针未交叉,则执行交换
{
int temp=q[i];
q[i]=q[j];
q[j]=temp;
}
//交换完成后,继续让i开始移动
}
//递归,将x区分开的两部分分别再次进行处理
quick_sort(q,l,j);
quick_sort(q,j+1,r);
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&q[i]);
}
quick_sort(q,0,n-1);
for(int i=0;i<n;i++)
{
printf("%d ",q[i]);
}
return 0;
}1.2第k个数
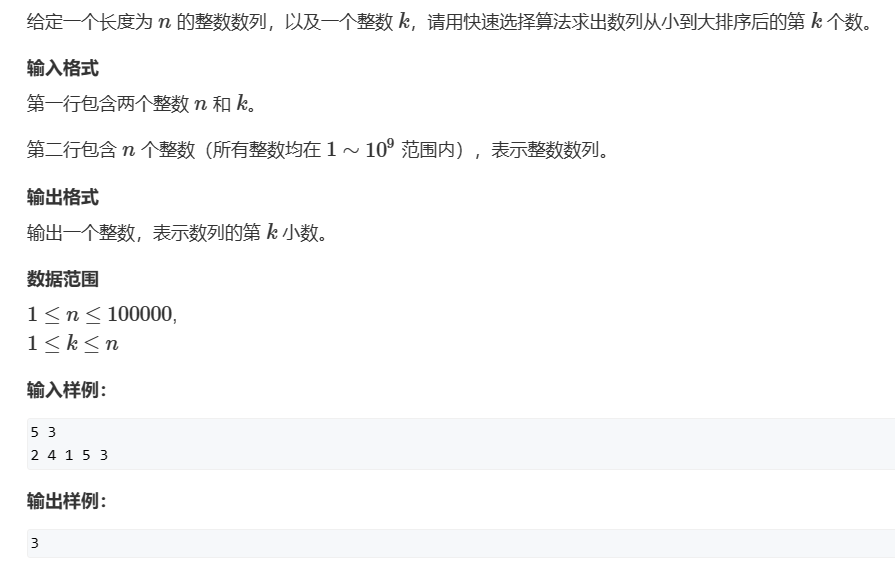
c++
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
int n, k;
cin >> n >> k;
vector<long long> aa(n);
for (int i = 0; i < n; i++) {
cin >> aa[i];
}
sort(aa.begin(), aa.end());
if (k <= n) {
cout << aa[k - 1] << endl;
}
return 0;
}2.归并排序
……
3.二分
……
4.高精度
4.1高精度加法

c++
#include <iostream>
#include <vector>
using namespace std;
const int N = 10e6+10;
vector<int> add(vector<int> &A, vector<int> &B)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || i < B.size(); i ++ )
{
if (i < A.size()) t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(1);
return C;
}
int main()
{
string a,b;
vector<int> A,B;
cin>>a>>b;
for(int i = a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
for(int i = b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
auto C = add(A,B);
for(int i = C.size()-1;i>=0;i--) {
printf("%d",C[i]);
}
return 0;
}4.2高精度减法

C++
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
bool cmp (vector<int> &A, vector<int> &B){
if (A.size()!=B.size()) return A.size() > B.size();
else{
for (int i = A.size() - 1;i>=0;i--){
if(A[i]!=B[i]){
return A[i]>B[i];
}
}
return true;
}
}
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a,b;
vector<int>A,B;
cin>>a>>b;
for(int i = a.size() - 1;i>=0;i--)A.push_back(a[i]-'0');
for(int i = b.size() - 1;i>=0;i--)B.push_back(b[i]-'0');
if(cmp(A,B)){
auto C = sub(A,B);
for(int i = C.size()-1;i>=0;i--) cout<< C[i];
}
else{
auto C = sub(B,A);
cout<<"-";
for(int i = C.size()-1;i>=0;i--)cout<< C[i];
}
return 0;
}4.3高精度乘法

4.3.1大数 * 小数
C++
#include <iostream>
#include <vector>
using namespace std;
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin>>a>>b;
vector<int> A;
for(int i = a.size() - 1 ;i >= 0;i--){
A.push_back(a[i]-'0');
}
auto C = mul(A,b);
for(int i = C.size()-1;i >= 0;i--){
cout<< C[i];
}
return 0;
}4.3.2大数 * 大数
c++
#include <iostream>
#include <vector>
using namespace std;
vector<int> mul(vector<int> A, vector<int> B)
{
vector<int> C(A.size() + B.size());
for (int i fo'r= 0; i < A.size(); i ++ )
for (int j = 0; j < B.size(); j ++ )
C[i + j] += A[i] * B[j];
for (int i = 0, t = 0; i < C.size() || t; i ++ )
{
t += C[i];
if (i >= C.size()) C.push_back(t % 10);
else C[i] = t % 10;
t /= 10;
}
while (C.size() > 1 && !C.back()) C.pop_back();
return C;
}
int main()
{
string a, b;
cin >> a >> b;
vector<int> A, B;
for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
auto C = mul(A, B);
for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
cout << endl;
return 0;
}4.4高精度除法

c++
#include<iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> div(vector<int> &A, int b,int & r) {
vector <int> C;
r = 0;
for(int i = A.size() - 1;i>= 0;i--){
r = r*10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(),C.end());
while(C.size() > 1&&C.back()==0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
int r;
cin>>a>>b;
vector<int> A;
for(int i = a.size()-1;i>=0;i--){
A.push_back(a[i]-'0');
}
auto C = div(A,b,r);
for(int i = C.size()-1;i>=0;i--){
cout << C[i];
}
cout<<endl<<r;
}5.前缀和与差分
5.1前缀和

c++
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int m,n;
int a[N],s[N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ){
scanf("%d", &a[i]);
}
for (int i = 1; i <= n; i ++ ){
s[i] = s[i-1] + a[i];
}
while (m -- ){
int l,r;
scanf("%d%d", &l, &r);
cout<<s[r]-s[l-1]<<endl;
}
}5.2子矩阵的和(二维前缀和)
5.2.1如何计算S[i,j]
S[i][j] = S[i - 1][j] + S[i][j- 1] - S[i - 1][j- 1] + a[i][j]
5.2.2如何计算(x1,y1),(x2,y2)这一子矩阵中所有数的和
S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1]

c++
#include <iostream>
using namespace std;
const int N = 1010;
int n,m,q;
int S[N][N],a[N][N];
int main()
{
scanf("%d%d%d",&n,&m,&q);
for (int i = 1; i <= n; i ++ ){
for (int j = 1; j <= m; j ++ ){
scanf("%d",&a[i][j]);
}
}
for (int i = 1; i <= n; i ++ ){
for (int j = 1; j <= m; j ++ ){
S[i][j] = S[i - 1][j] + S[i][j- 1] - S[i - 1][j- 1] + a[i][j];
}
}
while(q--){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d\n",S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1]);
}
}