重点摘要
梯度下降算法的实现
Pytorch解决梯度下降
优化器
利用PyTorch 定义神经网络模型类
学习代码
线性回归模型学习代码
lihuibear4/linea_regression (github.com)
常用库
numpy
NumPy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。
NumPy 的前身 Numeric 最早是由 Jim Hugunin 与其它协作者共同开发,2005 年,Travis Oliphant 在 Numeric 中结合了另一个同性质的程序库 Numarray 的特色,并加入了其它扩展而开发了 NumPy。NumPy 为开放源代码并且由许多协作者共同维护开发。
Matplotlib
Matplotlib 是 Python 编程语言及其数值数学扩展包 NumPy 的可视化操作界面
PyTorch基础
PyTorch中的所有操作都是在张量的基础上进行的, 本小节主要讲解张量的定义和相关张量操作以及GPU和张量之间的关系, 为以后使用PyTorch进行深度学习打下坚实的基础。
张量可以简单的看作是一个多维度的列表(List)。也可以将标量和向量看作张量,标量是零维的张量,向量是一维的张量,矩阵是二维的张量。
线性回归模型
线性回归是利用函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析简单来说,就是试图找到自变量与因变量之间的关系
1.案例-房价预测
分析
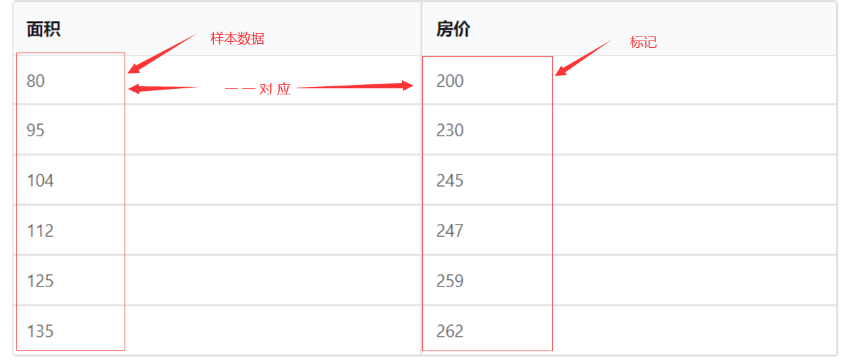

1.1预测模型的建立
下面先将已有的样本点在二维空间中描绘出来,看看是否符合线性规律。根据 data中的数据,绘制图形如下所示:
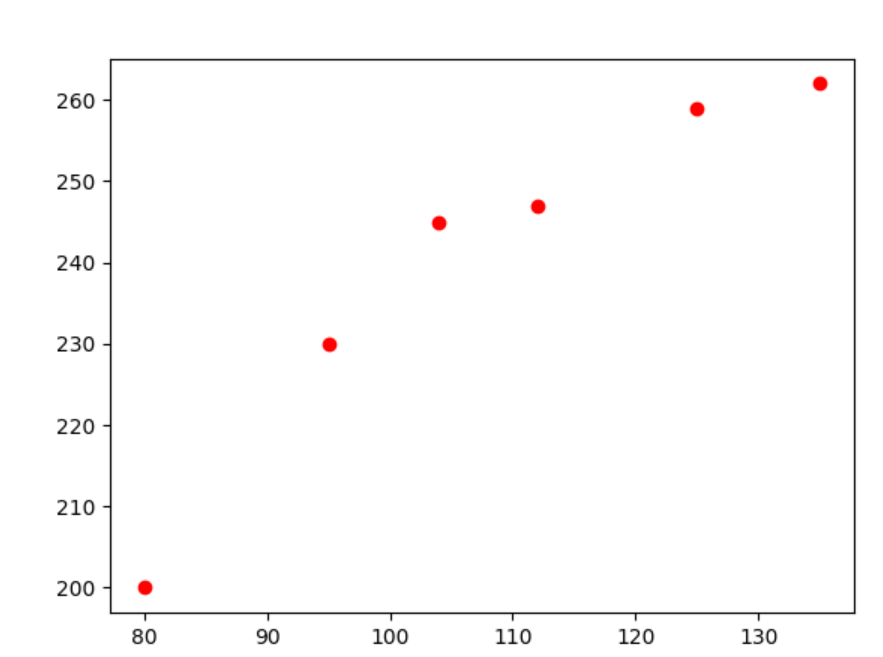
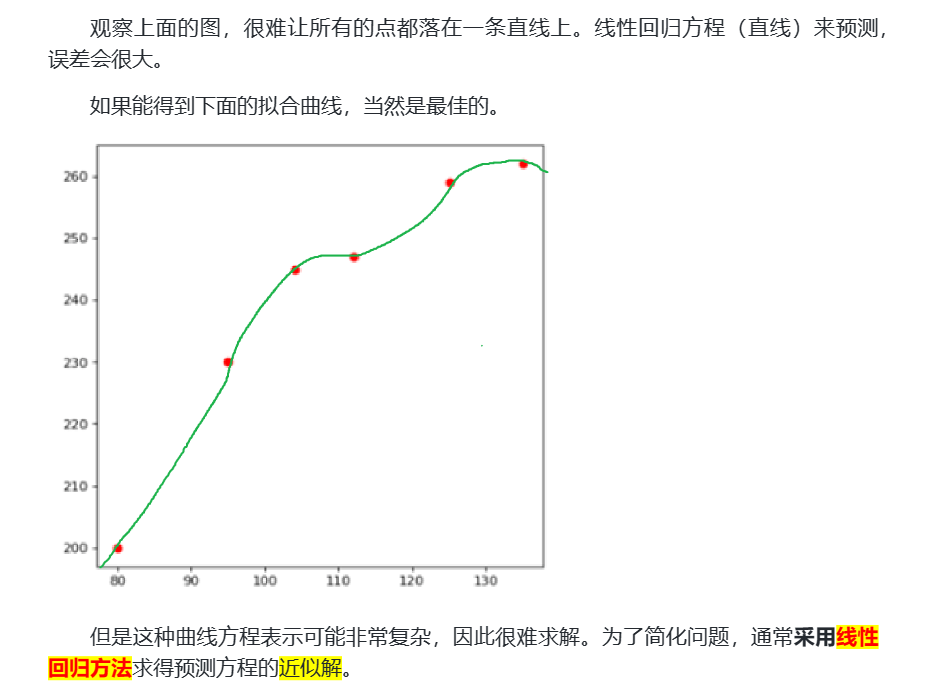
采用线性方程 f(x)=mx+b来拟合房价走势
其中,x为房屋的面积,f(x)为模型输出的预测价格对于预测模型,
发现和获得参数m和b的过程称为模型训练
1.1.1如何获得模型参数 m和 b 的值

1.1.2代码实现
import numpy as np
import matplotlib.pyplot as plt
import itertools
ms = []
bs = []
data = np.array(
[
[80,200],
[95,230],
[104,245],
[112,247],
[125,259],
[135,262]
]
)
X = data[:,0]
Y = data[:,1]
# 绘制图形
plt.scatter(X,Y,c="red")
plt.show()
com_lists = list(itertools.combinations(data,2))
# 两两存一组
for comlist in com_lists:
x1,y1 = comlist[0]
x2,y2 = comlist[1]
# 因有下列等式成立
# y1 = m * x1 + b
# y2 = m * x2 + b
#所以
m = (y2-y1) / (x2-x1)
b = y1 - m * x1
# or b = y2 - m * x2
ms.append(m)
bs.append(b)
m,b = np.mean(ms),np.mean(bs)
# 求平均值
print(ms,bs)
print(m,b)
print("=================")
x = 140
predict_fx =m * x + b
# 预测面积140的房价
print(f"140:{predict_fx}")2.模型训练知识准备
2.1均方误差

losses = []
for x,y in data:
predict = m * x + b
loss = (y-predict)**2
losses.append(loss)
print(losses)
print(np.mean(losses))
# 平均损失值:70.894644792979732.2梯度下降法引入

导(函) 数是一种变化率、是切线的斜率、是速度、是加速度。
导数的本质是通过极限的概念对函数进行局部的线性逼近(目标时获得极值)。
2.2.1一些常见函数的导数(导函数):
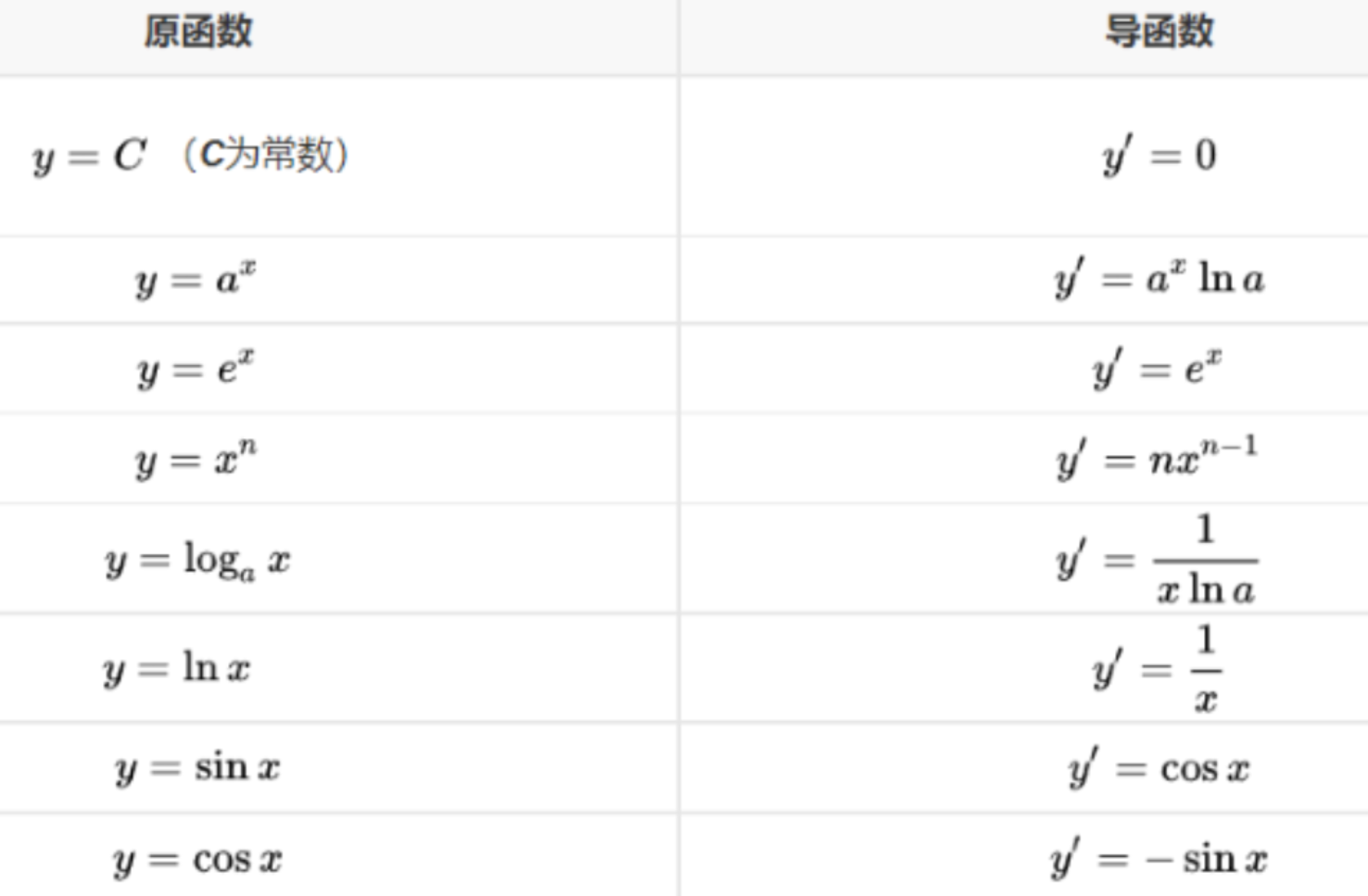
在机器学习中逐步逼近、迭代求解最优化时,经常会使用到梯度,
沿着梯度向量的方向是函数增加的最快,容易找最大值。
沿着梯度向量相反的地方,梯度减少的最快,容易找到最小值。

2.3梯度下降法公式推导

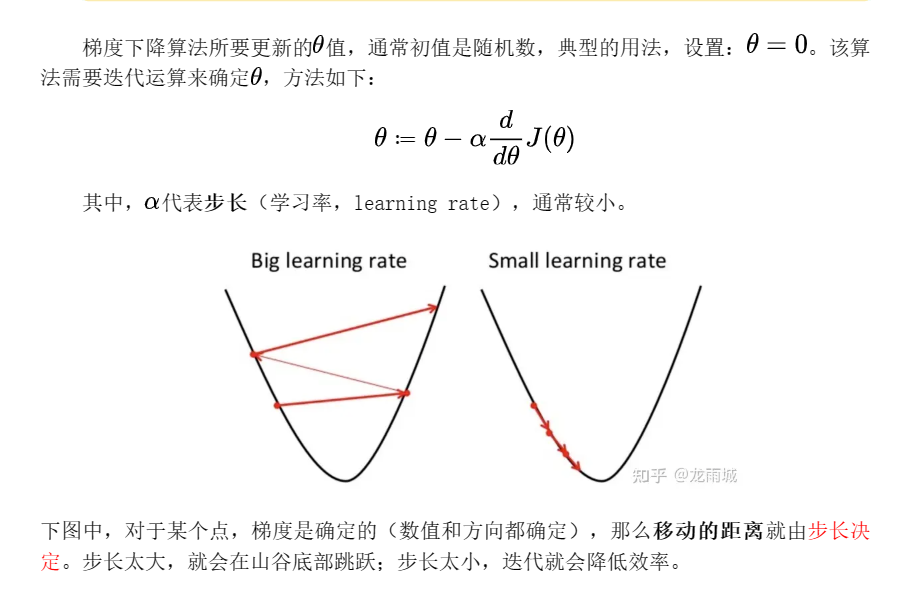
步长太大,就会在山谷底部跳跃;
步长太小,迭代就会降低效率。
2.4梯度下降算法的实现
- 首先,确定模型函数和损失函数(f(x)=mx+b,loss=MSE)
- 设定模型参数初始值和算法终止条件 (例如:m,b,lr,epoch)
- 开始迭代
- 计算损失函数的梯度(参数的偏导数)
- 求导

- 求导
- 步长乘梯度,得到当前位置下降的距离,更新参数
- 判断迭代过程是否终止(例如循环迭代次数满足),继续则跳转到步骤 3. 否则退出。
2.4.1代码实现
#梯度下降算法
import numpy as np
import matplotlib.pyplot as plt
import itertools
data = np.array(
[
[80,200],
[95,230],
[104,245],
[112,247],
[125,259],
[135,262]
]
)
# 初始化参数
m = 1
b = 1
lr = 0.00001
# 梯度下降的函数
# 当前的m,b和数据 data,学习率lr
def gradientdecent(m,b,data,lr):
loss,mpd,bpd = 0,0,0
# loss 均方误差 ,mpd为m的偏导数,bpd为b的偏导数
for xi,yi in data:
loss += (m * xi + b - yi)**2
bpd += (m * xi + b - yi) * 2
mpd += (m * xi + b - yi) * 2 * xi
#更新m,b
N = len(data)
loss = loss / N
mpd = mpd / N
bpd = bpd / N
m = m - mpd * lr
b = b - bpd * lr
return loss,m,b
for ecoch in range(30000000):
mse,m,b = gradientdecent(m,b,data,lr)
if(ecoch % 100000) == 0:
i= i + 1
print(f"第{i}次迭代+++loss={mse:.4f},m={m:.4f},b={b:.4f}")
# loss=42.8698,m=1.0859,b=122.67603.利用 PyTorch 进行梯度计算
3.1梯度的自动计算

3.1.1requires_grad
3.1.1.1参数配置
出现下面情况的原因是与loss2有关的设置中 requires_grad未设置,被默认为False,或者设置为了False
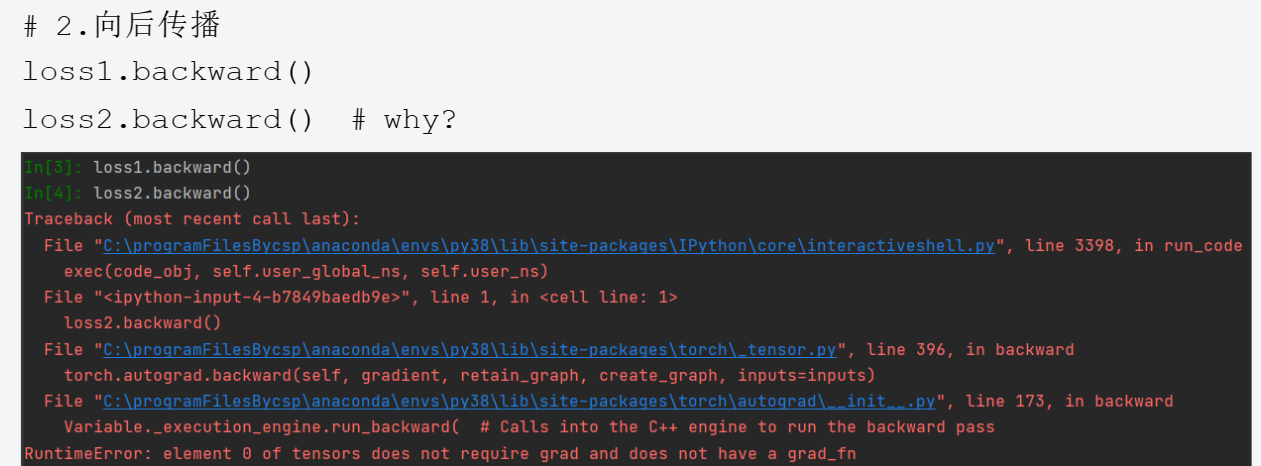
3.1.1.2requires_grad介绍

3.1.2代码演示
import torch
m1 = torch.randn(1,requires_grad=True)
m2 = torch.randn(1,requires_grad=False)
b1 = torch.randn(1)
b2 = torch.randn(1)
#%%
print(m1)
print(m2)
print(b1,b2)
#%%
def forward1(x):
global m1,b1
return m1 * x + b1
def forward2(x):
global m2,b2
return m2 * x + b2
data = [ [2,5] ] # m = 2 ,b =1 最佳
x = data[0][0]
y = data[0][1]
print(x,y)
#%%
# 1.前向传播,构建了计算图
predipt1 = forward1(x)
predict2 = forward2(x)
# 构造损失(代价)函数
loss1 = ( y - predipt1 ) ** 2
loss2 = ( y - predict2 ) ** 2
#%%
# 查看复合函数是否能够自动求偏导数
print(loss1.grad_fn)
print(loss2.grad_fn)
loss1.backward()
#%%
#查看m1和m2的偏导值
print(m1.grad,b1.grad,m2.grad)
print(m1.grad)
print(m2.grad)
#%%
mpd1 = 2 * (y - (m1 * x +b1)) * (-1 * x )
print(mpd1)
print((mpd1 == m1.grad))简单来说向前传播是为了计算损失函数,向后传播是为了计算梯度
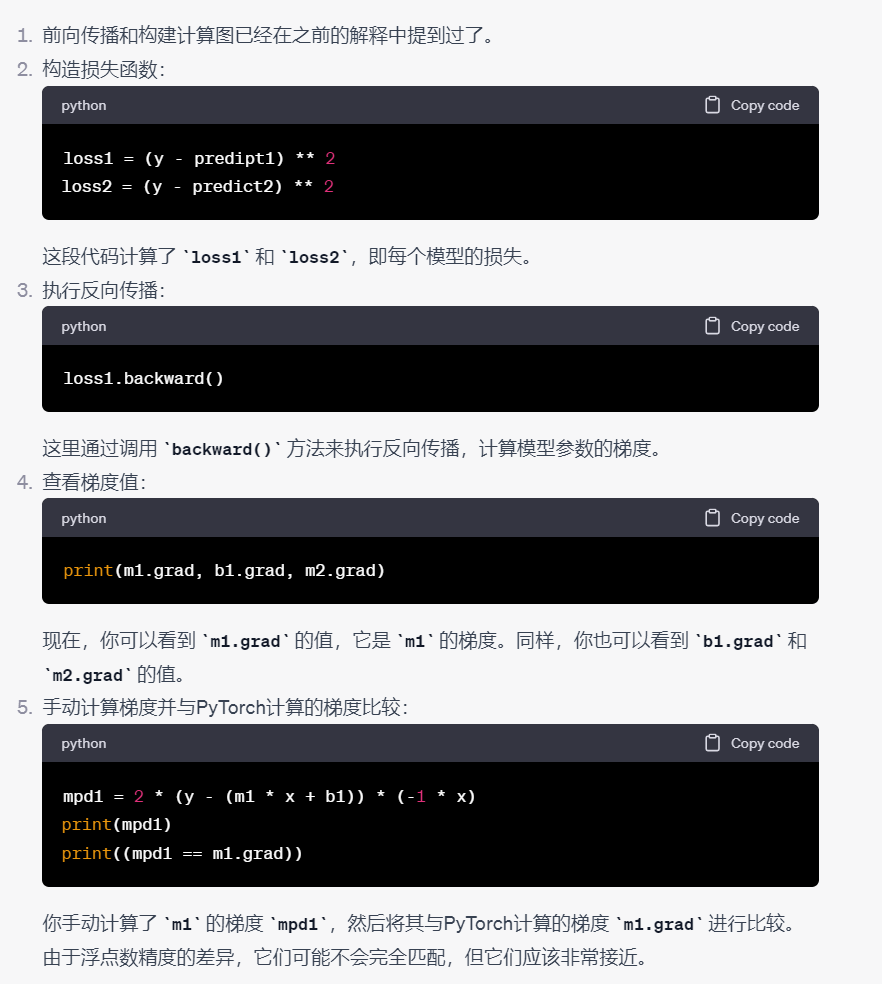
3.2多层神经网络的梯度计算

# 多层神经网络计算梯度案例
# x中的特征数据批量定义,batch=3
import torch
x = torch.randn(3,requires_grad=True)
#x = {x1,x2,x3}
# 第二层定义
y = x + 2
# 输出层定义
z = 3 * y ** 2 # 3倍的y的平方
#建立J函数,可向后传播(此处J=z.mean(),该函数无实际意义
z = z.mean() # z = (z1+z2+z3)/3 只有标量可以向后传播
#%%
print(x)
print(y)
print(z)
#%%
z.backward()
print(x.grad)
print(2 * (x + 2))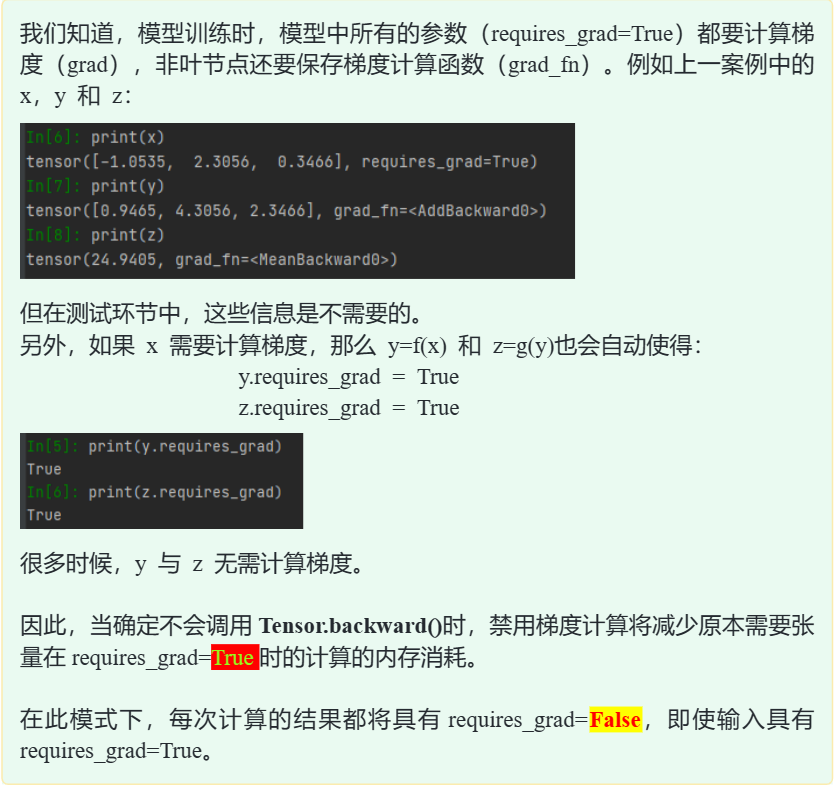
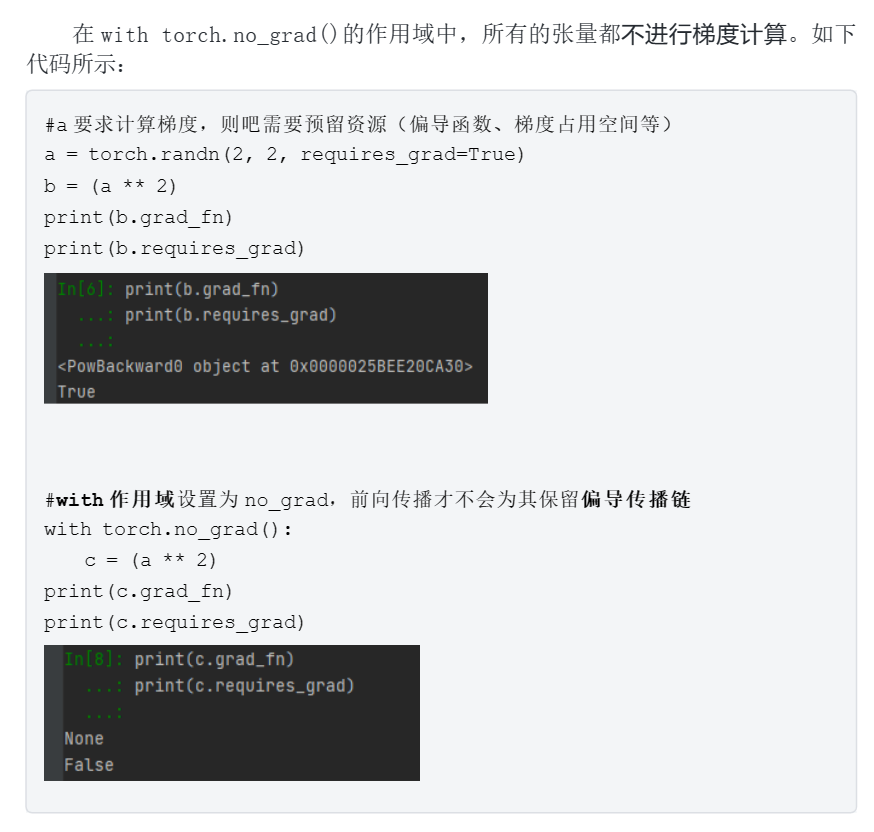
3.3梯度清空
3.3.1梯度清空
为了避免累加,通常计算梯度后,先清空梯度,再进行其他张量的梯度计算。 PyTorch 中,使用 grad.zero_0 清空梯度。
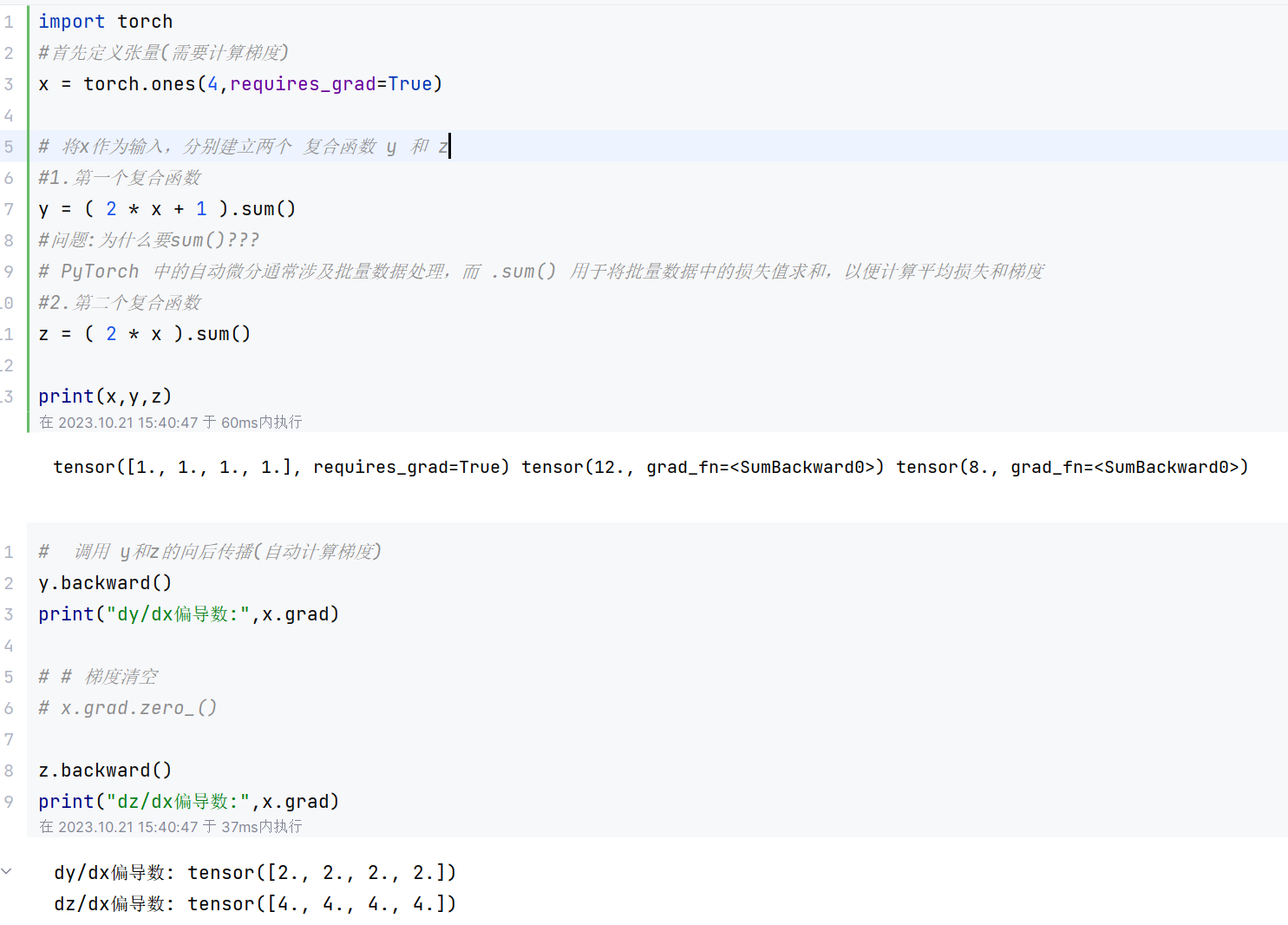
3.3.2梯度清空后

3.4正向和向后传播的函数定义
神经网络本质上是一个非常复杂且有大量参数的复合函(函数链条)
3.4.1前向传播
在 PyTorch 中,前向传播就是通过函数的定义来构建计算图(传播链条),形成神经网络的基本框架,并得到神经网络的输出(预测值)。
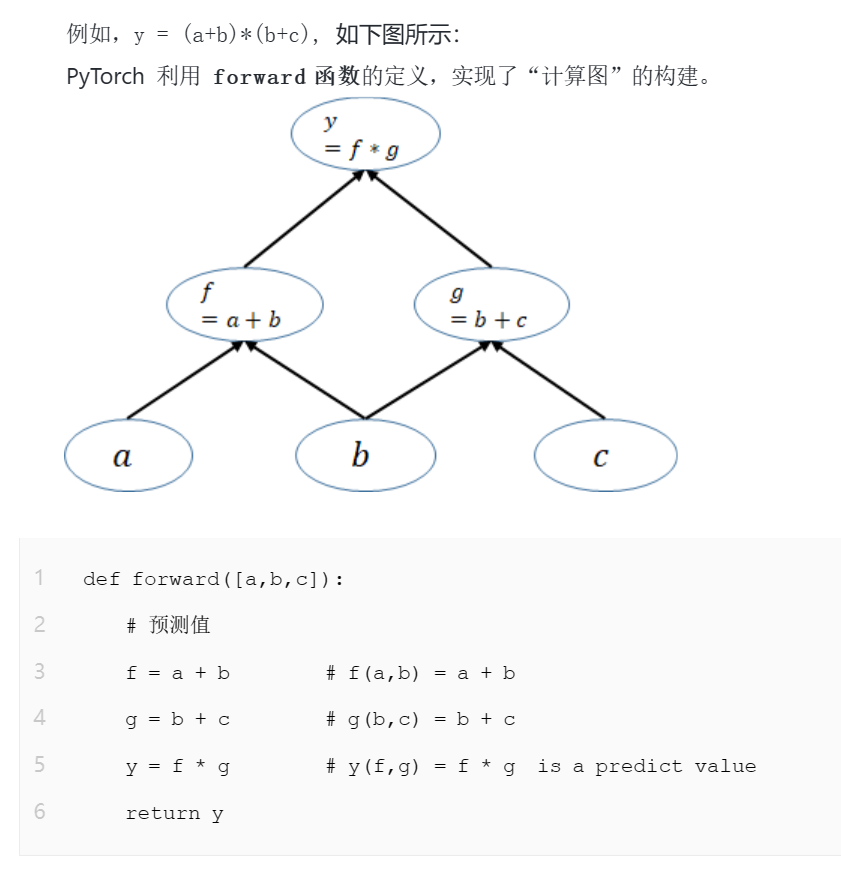

3.4.2向后传播
根据计算图,在向后传播过程,通过计算参数 w的梯度,并不断选代更新参数 w,目标是使J(代价)函数获得最小值。如下图所示:
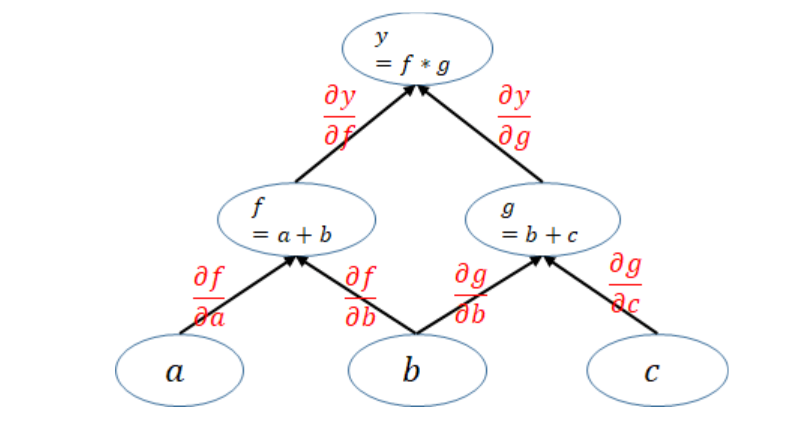
3.4.3总结
- 前向传播算法定义神经网络 (计算图)初始参数为随机数(一次性)
- 向后传播算法优化迭代更新模型的参数值(多次),获得最优模型:
3.5模型训练的问题及优化
训练模型的过程,就是不断迭代,在向后传播过程中,不断采用梯度下降方法计算模型参数的梯度方向,并沿着该方向不断迭代,以修正模型的参数,目标是使得损失函数结果为最小,这个过程就是寻找最优参数值的过程。
3.5.1模型训练过程包括以下步骤:
- 正向传播
- 计算损失
- 向后传播
- 更新参数
- 清空梯度
3.6使用PyTorch进行模型训练
PyTorch 中,已有很多封装好的损失函数可以直接利用
3.6.1PyTorch中常用的损失函数
- 均方差损失函数 (MSELoss): 计算预测值(Predict) 和标记值(Labe1) 之差的均方差
torch.nn.MSELoss - 交叉熵损失 (CrossEntropyLoss) 在多分类任务中,交叉熵描述了预测分类和标记间不同概率分布的差异
torch.nn.CrossEntropyLoss() - 二进制交叉熵损失(BCELoss) 二分类任务时的交叉熵计算函数
torch.nn.BCELoss()
3.6.2优化器
优化器的目标就是:根据损失函数,找到更新参数的最优方法或路径
3.6.2.1使用优化器的原因
- 通常,只要损失函数是凸函数,就一定能找到全局最小值。但是现实情况是,神经网络复杂结构,常常使损失函数不具备凸性,不能简单使用凸函数的最优化技巧就能解决问题的。
- 训练数据集的规模越大,利用所有样本计算梯度的代价就越大。
- 避免在向后传播过程中,梯度下降方法陷入局部最优
PyTorch 封装了数个实用的优化方法(优化器)。通常来说,不同任务选择不同优化器常用的优化器有以下几种:
3.6.2.2优化器类型
- 随机梯度下降法 (stochastic gradient descent,SGD)

- optim.Adagrad: 自适应学习率梯度下降法
- optim.RMSprop: Adagrad 的改进
- optim.Adadelta: Adagrad 的改进
- optim.Adam: RMSprop 结合 Momentum
- optim.Adamax: Adam 增加学习率上限
- optim.SparseAdam: 稀疏版的 Adam
- optim.ASGD: 随机平均梯度下降
- optim.Rprop: 弹性向后传播
- optim.LBFGS: BFGS 的改进
3.6.2.3优化器
我们可以通过下面方式定义一个 SGD 优化器
optimizer = torch.optim.SGD([W],lr = learning_rate)其中,第一个参数张量 [w] 为模型中要更新的参数,第二个 1r 为学习率(步长)。 优化器可一次性对所有模型参数变量进行更新,免去手动更新参数的繁琐(Impossible Mission 不可能完成的任务)。函数如下:
optimizer.step() #根据参数梯度,对模型中的参数进行更新
optimizer.zero_grad() #清空模型参数梯度,防止累计情况发生3.6.2.4代码实战
import torch
import torch.nn as nn
X = torch.tensor([1,2,3,4],dtype=torch.float32)
Y = torch.tensor([2,4,6,8],dtype=torch.float32)
W = torch.tensor(0.0,dtype=torch.float32,requires_grad=True)
#向前传播
def forward(X):
return W * X
# pytorch方法调用MSE损失函数
loss = torch.nn.MSELoss()
learning_rate = 0.01
n_iters = 100
loss = nn.MSELoss()
optimizer = torch.optim.SGD([W],lr = learning_rate)
print(optimizer)
for epoch in range(n_iters):
# 1.正向传播
y_pre = forward(X)
#2.计算损失
l = loss(Y,y_pre)
# 3.向后传播 (计算梯度)
l.backward()
#4.更新权重,即向梯度反方向走一步,由优化器完成
# 与之前对比,好处是只需要使用优化器的方法即可,多个参数只要一个语句
optimizer.step()
#5.清空梯度,由优化器完成
optimizer.zero_grad()
if epoch % 10 == 0:
print(f"epoch:{epoch},w={W},loss={l:.8f}")3.6.3模型定义
当设计复杂神经网络时,开发者可以使用 PyTorch 中的积木构件(常用函数封装),进行自由拼装,来构建神经网络模型。
例如,线性函数常用来作为神经网络中的全连接层,在 Ptorch 中封装为:
torch.nn.Linear(input features,output features
函数形式:f(x)=wx+ b
数据特征:x =[x1,X2,...,Xx]
模型参数:w=[wi,W2,..·,Wx分类,或回归 output_features = 1, 否则> 1
使用 PyTorch 可以极大的简化我们编程的难度损失函数和优化器的定义形式,就能快速搭建神经通常只需要改变模型、网络模型,进行训练以解决不同的深度学习问题。
4.利用PyTorch 定义神经网络模型类
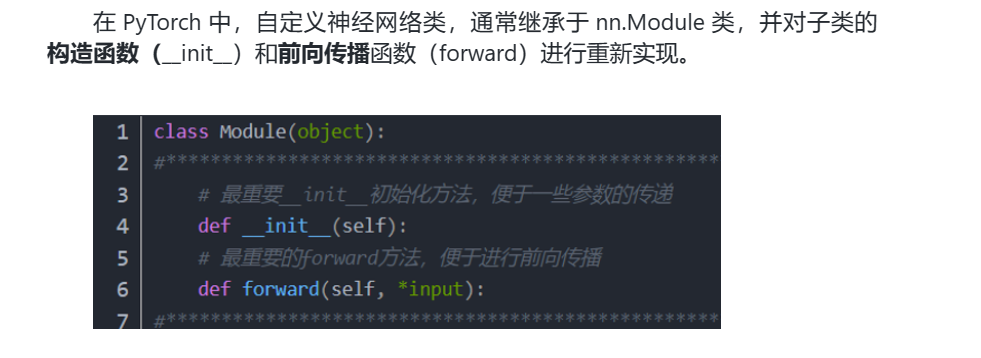
4.1利用sklearn 生成模拟数据
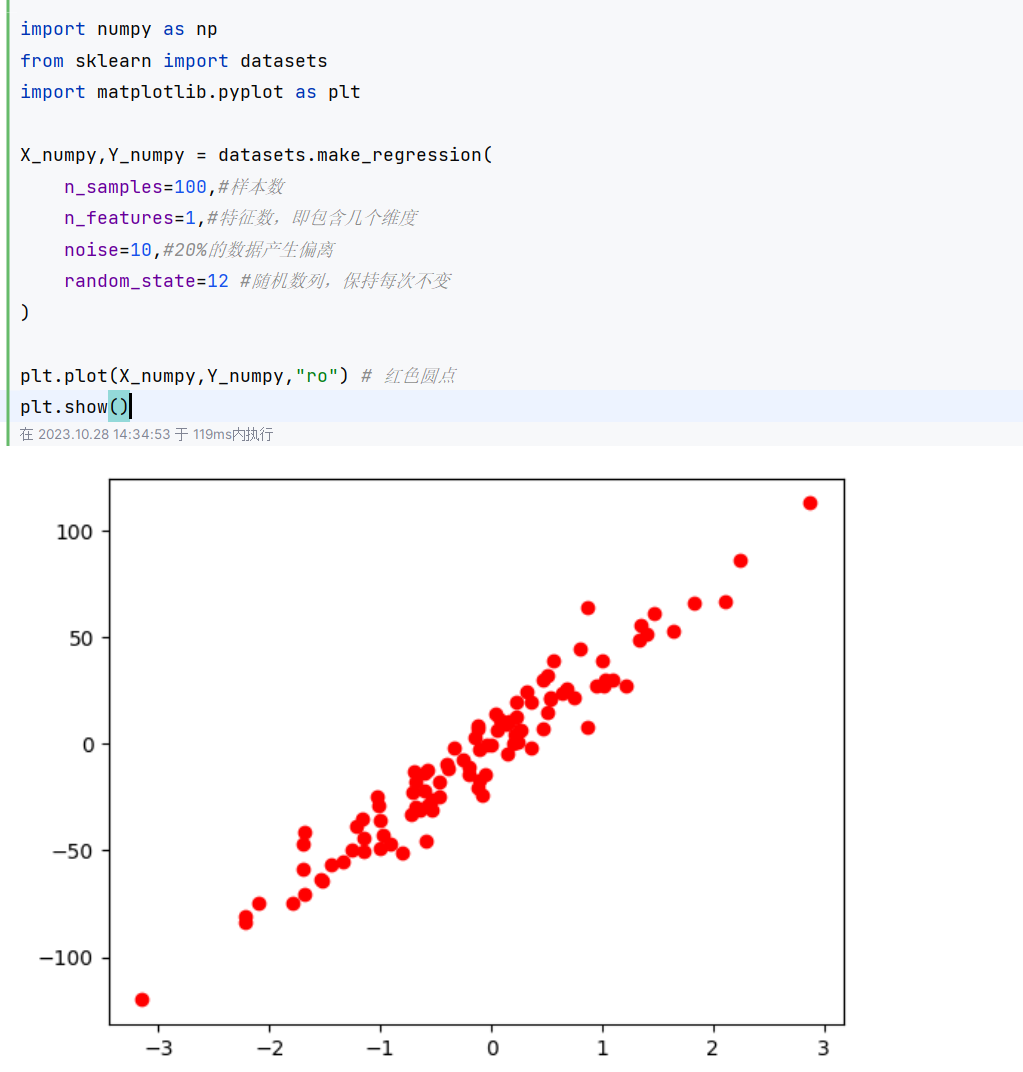
4.2神经网络的定义
注意
numpy产生的浮点数默认为64位,即double型
pytorch浮点数为32位
使用时通过astype转换为32位



